Fellows (1st-term)

Biography

2011 　Research Fellow of the Japan Society for the Promotion of Science (DC2)
2012 　Graduate School of Fundamental Science and Engineering, Waseda University (Phd, Doctor of Science)
2012 　Research Fellow of the Japan Society for the Promotion of Science (PD)
2013 　Assistant professor, Department of Applied Mathematics, Waseda University
2015 　Junior researcher, Research Institute for Science and Engineering, Waseda University
2016 　Assistant professor, Faculty of Engineering, Information and Systems, University of Tsukuba

Research Outline

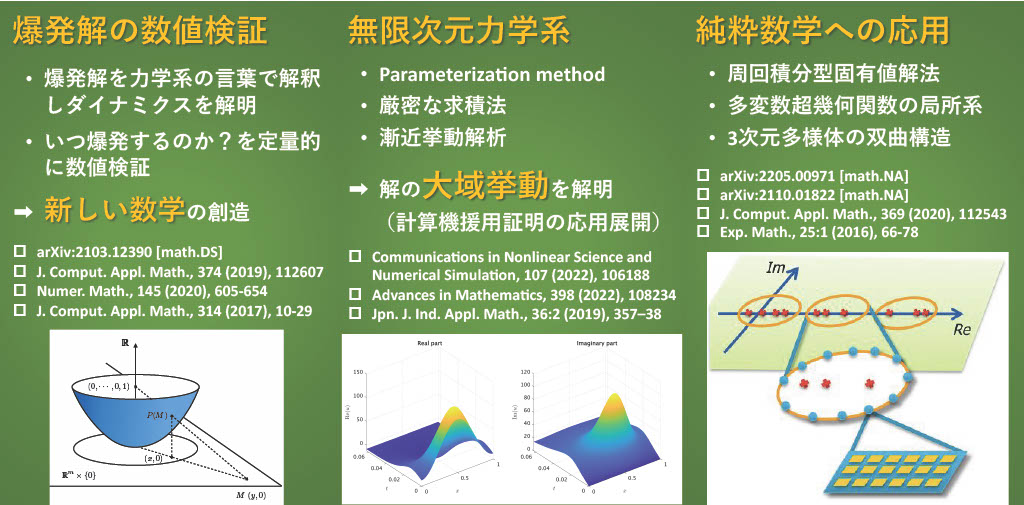
Rigorous numerics is a numerical method based on interval arithmetic, which takes all errors of numerical computations into account. It yields mathematically rigorous result using numerical computations. The main interest of my research is the development of rigorous numerics for solutions of differential equations (partial differential equations, delayed differential equations, ordinary differential equations). Many phenomena in physics, chemistry, biology, and other fields are often described by differential equations. However, solving differential equations is often very difficult. When seeking solutions to differential equations, we first approximate the equation and then use the approximate solution obtained as a guide to the exact solution. In my research, we take such an approximate solution by numerical computations, and verify that the exact solution exists uniquely in the neighborhood of the approximate solution. This enables us to prove the existence of solutions to unsolved problems.

Many researchers have devoted themselves to development of rigorous numerics especially for nonlinear elliptic partial differential equations. We have developed a theory of rigorous numerics for initial-boundary value problems of time evolutionary equations using semigroup theory (analytic semigroup and the evolution operator) in mathematical analysis and engaged in research on computer-assisted proofs as an effective combination of mathematical analysis and rigorous numerics.

What is my goal as a transborder researcher?

自分の殻に閉じ籠らず、世界を相手に自分の手を動かして研究成果を生み続ける研究者

I would like to be researchers who do not go inside their own shell, try to challenge against the world, and continue to get research results by working with their own hands.