筑波大学
システム情報系
准教授
Associate Professor
Institute of Systems and Information Engineering
University of Tsukuba
2011年4月 日本学術振興会 特別研究員 DC2
2012年3月 早稲田大学大学院基幹理工学研究科数学応用数理専攻 博士後期課程 修了 博士（理学）
2012年4月 日本学術振興会 特別研究員 PD
2013年4月 早稲田大学 基幹理工学部 応用数理学科 助教
2015年4月 早稲田大学 理工学術院 総合研究所 次席研究員
2016年4月 筑波大学 システム情報系 助教
2011 Research Fellow of the Japan Society for the Promotion of Science (DC2)
2012 Graduate School of Fundamental Science and Engineering, Waseda University (Phd, Doctor of Science)
2012 Research Fellow of the Japan Society for the Promotion of Science (PD)
2013 Assistant professor, Department of Applied Mathematics, Waseda University
2015 Junior researcher, Research Institute for Science and Engineering, Waseda University
2016 Assistant professor, Faculty of Engineering, Information and Systems, University of Tsukuba
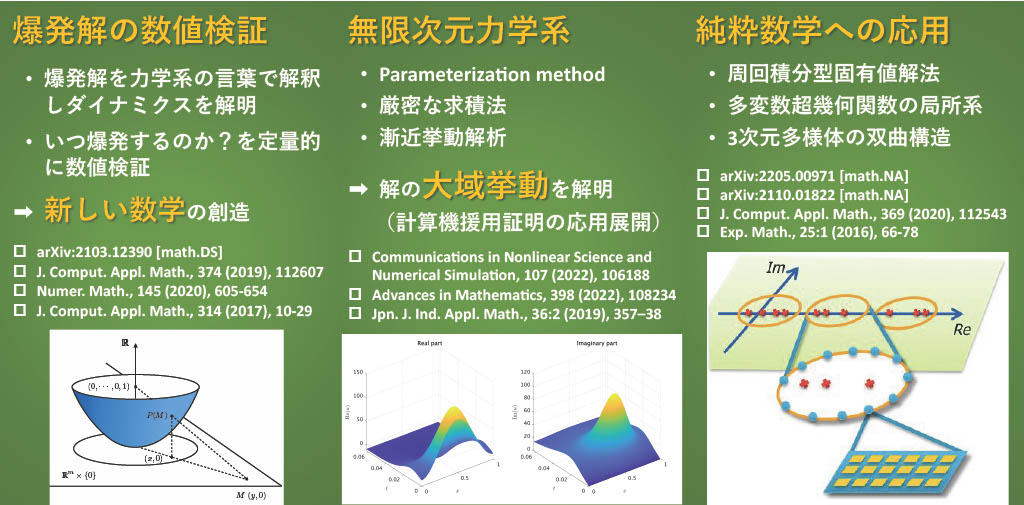
数値計算に生じるすべての誤差を把握し、数学的に正しい結果を数値計算によって導く計算法を「精度保証付き数値計算」といいます。私の研究の主なテーマは、微分方程式（偏微分方程式, 遅延微分方程式, 常微分方程式）に対する解の精度保証付き数値計算法の開発です。物理、化学、生物などの諸分野における多くの現象は微分方程式で記述されることが多く、これを解く事が求められます。しかし、微分方程式を厳密に解くことは多くの場合大変難しいです。微分方程式の解を求める場合、まず方程式の近似を考え、得られた近似解を指針にもとの解を得る方法が一般的に考えられます。私の研究では、方程式を解く指針として数値計算で得られた近似解をとり、その近傍に解が一意存在することを数値計算によって検証します。これにより厳密に解く事が難しい問題も精度保証付き数値計算を用いる事で解の存在を証明できるようになります。
これまで多くの研究者が特に偏微分方程式に対する解の精度保証付き数値計算法の開発に尽力され、非線形楕円型偏微分方程式に対する数値解の検証が可能となりました。私は数理解析学における半群理論（解析半群および発展作用素）を用いた時間発展方程式の初期値境界値問題に対する解の精度保証付き数値計算手法を開発し、数理解析理論と精度保証付き数値計算の効果的な融合成果として計算機援用証明の研究に従事しています。
Rigorous numerics is a numerical method based on interval arithmetic, which takes all errors of numerical computations into account. It yields mathematically rigorous result using numerical computations. The main interest of my research is the development of rigorous numerics for solutions of differential equations (partial differential equations, delayed differential equations, ordinary differential equations). Many phenomena in physics, chemistry, biology, and other fields are often described by differential equations. However, solving differential equations is often very difficult. When seeking solutions to differential equations, we first approximate the equation and then use the approximate solution obtained as a guide to the exact solution. In my research, we take such an approximate solution by numerical computations, and verify that the exact solution exists uniquely in the neighborhood of the approximate solution. This enables us to prove the existence of solutions to unsolved problems.
Many researchers have devoted themselves to development of rigorous numerics especially for nonlinear elliptic partial differential equations. We have developed a theory of rigorous numerics for initial-boundary value problems of time evolutionary equations using semigroup theory (analytic semigroup and the evolution operator) in mathematical analysis and engaged in research on computer-assisted proofs as an effective combination of mathematical analysis and rigorous numerics.
自分の殻に閉じ籠らず、世界を相手に自分の手を動かして研究成果を生み続ける研究者
I would like to be researchers who do not go inside their own shell, try to challenge against the world, and continue to get research results by working with their own hands.